Model Resolution » Gridpoint Equivalency of Spectral Resolution

It takes about five to seven grid points to get reasonable approximations of most weather features. Still more points per wave feature are often necessary to get a good forecast. Because spectral and gridpoint models preserve information in different ways, no precise equivalent grid spacing can be given for a spectral model resolution.

The approximate grid spacing with the same accuracy as a spectral model can then be represented as ΔX ~ 360° / 3N; where N is the number of waves.

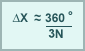
For a T80 model, this results in maximum grid spacing for equivalent accuracy of about 1.5° ~ 160 km (assuming 1° ~ 111 km).

We can approximate the grid spacing to obtain equivalent accuracy to a spectral model with a fixed number of waves using a simple approach. First, we assume that three grid points are sufficient to capture the information contained in each of a series of continuous waves. This is demonstrated by the figure below, where a wavelike feature may be captured by three blue dots to produce the square wave shown, and post processed to the yellow wave.

The dynamics of spectral models retain far better wave representation than gridpoint models with this grid spacing. However, the spectral model physics is calculated on a grid, with about three times as many grid lengths as number of waves used to represent the data. Since it takes five to seven grid points to represent 'wavy' data well and even more for features that include discontinuities, the resolution of the physics is poorer than the above formulation indicates and degrades the quality of the spectral model forecast.